从 Largest Rectangular Area in a Histogram 说开去

这是 LeetCode 上的一道算法题，以下内容是我在解这道题的思路和这道题的一个应用。

题目

Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

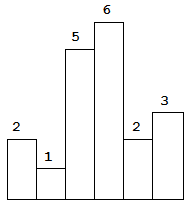
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].
The largest rectangle is shown in the shaded area, which has area = 10 unit.

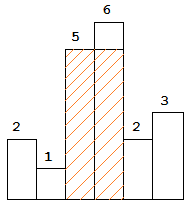
For example,
Given height = [2,1,5,6,2,3],
return 10.

简单的说就是：已知直方图每一根柱子的高度，求其能组成的长方形的最大面积。

思路

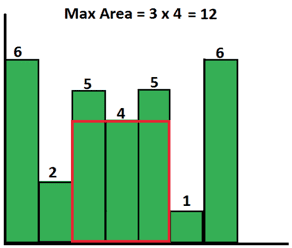
最大的矩形面积，其高度一定是其中的一根最低的柱子的高度，例如：

最低柱子：高度为 5 的柱子（第 3 根柱子）

最低柱子：高度为 4 的柱子（第 4 根柱子）

所以，最终的结果一定是：

max(以第 i 根柱子为最低柱子的最大矩形面积)，0 <= i <= n

所以，问题就变成了：如何计算以第i根柱子为最低柱子的最大矩形面积？

计算以第`i`根柱子为最低柱子的最大矩形面积`Si`

记第i根柱子的高度为 height[i];

计算以第i根柱子为最低柱子的最大矩形面积Si，高度已经知道，是height[i]；还需要计算其底边长：

从第i根柱子开始：

向左算出第一根高度小于height[i]的柱子，记其下标为left_index；
向右算出第一根高度小于height[i]的柱子，记其下标为 right_index。

则底边长 = (right_index - left_index - 1)，所以：
Si = height[i] * (right_index - left_index - 1)。

例如：

对于第 4 根柱子（高度height[4] = 4），向左第一根高度小于height[4]的柱子是第 2 根柱子，其高度为 2；向右第一根高度小于height[4]的柱子是第 6 根柱子，其高度为 1；所以 S4 = 4 * (6 - 2 - 1) = 12

从左到右遍历所有柱子，遍历到第i根柱子时，如果要计算Si，其左边界容易确定，但右边界是第i根柱子右边的柱子，无法确定，所以无法计算面积Si。

换个思路，遍历到第i根柱子时，所有以第i根柱子为右边界的柱子j(0 < j < i) 的右边界就确定了，所以Sj就能够计算了。

哪些柱子会以第i根柱子为右边界？肯定是高度大于height[i]的柱子。

使用一个栈s来存储无法确定右边界的柱子的下标，进行以下操作：

当栈为空时，将i入栈：s.push(i)，i++
当 height[i] >= 栈顶元素的高度，将i入栈：s.push(i), i++
当height[i] < 栈顶元素的高度，说明第i根柱子是当前栈顶元素 (也就是第 s.top() 根柱子) 的右边界，所以可以计算其面积：
- right_index = i
- left_index = 当前栈顶下的第一个元素；只需执行以下操作：
- s.pop();
- left_index = s.top();

实现

具体代码如下：

int largestRectangleArea(vector<int> &height) {
    int n = height.size();
    int i = 0;
    int max_area = 0;  // 最大面积
    stack<int> s;
    while (i < n) {
        if (s.empty() || height[i] >= height[s.top()]) {
            // 如果栈为空或者 height[i] >= 栈顶元素的高度,将 i 进栈
            s.push(i);
            i++;
        } else {
            int current = s.top(); / 当前要计算面积的柱子的下标
            s.pop();

            // 左边界，如果栈为空，则以第一根柱子前一位为左边界
            // 在这里第一根柱子下标为0，所以以 -1 为左边界
            int left_index = s.empty() ? -1 : s.top();
            int current_area = height[current] * (i - left_index - 1);  // 右边界 == i

            if (current_area > max_area) {
                // 如果当前计算面积比之前计算的所有面积都大,则更新最大面积
                max_area = current_area;
            }
        }
    }


    while (!s.empty()) { // 计算栈中剩余元素的面积
        int current = s.top();
        s.pop();
        int left_index = s.empty() ? -1 : s.top();
        int current_area = height[current] * (i - left_index - 1);

        if (current_area > max_area) {
            max_area = current_area;
        }
    }

    return max_area;
}

简化代码

如果给最后加上一个元素元素 0 作为所有柱子的右边界，则在while (i < n)循环结束后栈一定是空的，可以简化代码如下：

int largestRectangleArea(vector<int> &height) {
	height.push_back(0); // 最后加上一个元素 0 作为所有柱子的右边界
    int n = height.size();
    int i = 0;
    int max_area = 0;  // 最大面积
    stack<int> s;
    while (i < n) {
        if (s.empty() || height[i] >= height[s.top()]) {
            // 如果栈为空或者 height[i] >= 栈顶元素的高度,将 i 进栈
            s.push(i);
            i++;
        } else {
            int current = s.top(); // 当前要计算面积的柱子的下标
            s.pop();
            int left_index = s.empty() ? -1 : s.top();  // 左边界
            int current_area = height[current] * (i - left_index - 1);  // 右边界 == i

            if (current_area > max_area) {
                // 如果当前计算面积比之前计算的所有面积都大,则更新最大面积
                max_area = current_area;
            }
        }
    }
    return max_area;
}

应用

LeetCode 上的另一题：Maximal Rectangle

Given a 2D binary matrix filled with 0’s and 1’s, find the largest rectangle containing all ones and return its area.

一开始看这个题目以为是要计算包含了所有1的长方形的最大面积，那这样取最大的不就好了？显然题目不是这意思，题目的意思是长方形全部由1组成，求这样的长方形的最大面积。

从上到下遍历每一行，对于第i行，只要计算出每一列的高（相当于前面所说的每根柱子的高），就能按照之前的方法计算出最大面积。

计算出每一列的高

用i表示当前行，用j表示当前列，用height[i][j]表示其高度

如果 matrix[i][j] == '0'，则height[i][j] = 0
如果 matrix[i][j] == '1'：
- 如果当前是第一行，则height[i][j] = 1
- 否则：height[i][j]等于前一行当前列的高度加 1，也就是：height[i][j] = height[i - 1][j] + 1

其实只需要用一维数组height[j]表示高度，因为在计算height[j]时，其值就等于前一行当前列的高度，也就是：height[j] = height[j] + 1。对于第 1 行，只需将height[j]全部初始化为 0 即可。

具体代码如下：

int maximalRectangle(vector<vector<char> > &matrix) {
    int numRows = matrix.size();  // 行数
    if (numRows <= 0) {
        return 0;
    }
    int numColumns = matrix[0].size();  // 列数
    int max_area = 0;
    int * height = new int[numColumns + 1];
    memset(height, 0, numColumns * sizeof(int)); // 将height初始化为 0
    height[numColumns] = -1;  // 最后加上元素 -1 作为所有元素的右边界

    for (int i = 0; i < numRows; ++i) {  // 遍历每一行
        for (int j = 0; j < numColumns; ++j) {
            height[j] = (matrix[i][j] == '1') ? height[j] + 1 : 0;
        }
        int j = 0;
        stack<int> s;
        while (j <= numColumns) {

            if (s.empty() || height[j] >= height[s.top()]) {
                // 如果栈为空或者 height[j] >= 栈顶元素的高度,将 j 进栈
                s.push(j);
                j++;
            } else {
                int current = s.top(); // 当前要计算面积的柱子的下标
                s.pop();
                int left_index = s.empty() ? -1 : s.top();  // 左边界
                int current_area = height[current] * (j - left_index - 1);  // 右边界 == j

                if (current_area > max_area) {
                    // 如果当前计算面积比之前计算的所有面积都大,则更新最大面积
                    max_area = current_area;
                }
            }
        }
    }

    delete[] height;
    return max_area;
}

参考资料

[1] https://www.geeksforgeeks.org/largest-rectangle-under-histogram/

从 Largest Rectangular Area in a Histogram 说开去

题目

思路

计算以第i根柱子为最低柱子的最大矩形面积Si

实现

简化代码

应用

计算出每一列的高

计算以第`i`根柱子为最低柱子的最大矩形面积`Si`